Below is an image of a square, 7 cm to a side, with four quarter-circles inscribed into it as showm.
Find the area of the shaded region in the center.
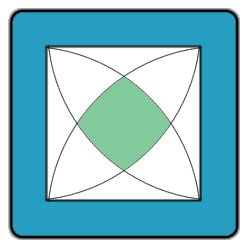
Construct the equilateral triangle inside the top-left Reuleaux-type shape.This is part of a pie-slice with its point in the bottom left corner. Since can we fit three slices in the quarter pie going from to left to bottom right, each pie-slice is clearly 1/12 of the whole pie, i.e. 49π/12.
If we cut the circular segment off the pie slice, we have an isoceles triangle enclosing the equilateral triangle. The Reuleaux-type shape in the top left-hand corner is just the same as the one we already looked at. Draw an identical equilateral triangle in it. Now consider the top space between the two equilateral triangles. It's just the same shape as the two triangular pieces of the isoceles triangle enclosing the first equilateral triangle.
So 4 of those isoceles triangles have the same area as the whole square; 49 square units.
But in that case, the circular segment we cut off is simply 49π/12 - 49/4.
The side length of the square is the same as the side length of the equilateral triangles. Wikipedia gives 2 sin (theta/2) as the equation for the equivalent chord. sin (π/24) = (sqrt(3) - 1)/(2 sqrt(2)), so the length is (7 (sqrt(3) - 1))/sqrt(2). Then the square has an area of 49 (2 - sqrt(3)).
Thus the required green area is 49 (2 - sqrt(3))+ 49π/3-49 = 49 (1 - sqrt(3) + π/3)
Edited on December 29, 2016, 9:06 pm
|
|
Posted by broll
on 2016-12-29 10:33:21 |



