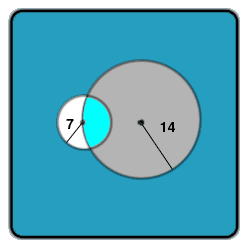
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.

(P.S -The answer might not be elegant)

Lucky's solution matches one I've found by a different method.
Triangle ASL can be solved for the angles at S and at L, the centers of the two circles, by using the law of cosines:
Calling angle ASL, S for brevity, and ALS, L,
14²=14²+7²-2(14)(7)cos(S)
and 7²=14²+14²-2(14)(14)cos(L)
Solving for the angles, ASL = arccos(14) and ALS = arccos(7/8). The angles that subtend the common chord are twice these angles, and the pie slices are the fraction of the respective circles represented by these doubled angles. From these we have to subtract the triangles formed by the chord and the radii to the ends of the chord. Each of those triangles is isosceles and so formed from two right triangles. One has base 7*.25 (from A=arccos(.25)) and the other has base 14*(7/8). The vertical leg of each can be found by sin²x+cos²x=1, i.e., 7(√(1-.25²)) and 14(√(1-(7/8)²))
We then get
7²arccos(.25)-7²(√(1-.25²))/4 + 14²arccos(7/8) - (7/8)14²√(1-(7/8)²)
and indeed this comes out to 68.750255544601..., matching lucky's answer.

Posted by Charlie on 2003-02-11 05:35:26