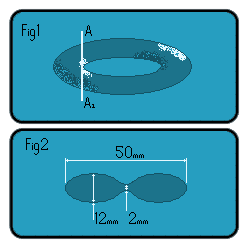
Take a regular torus (doughnut) shaped object and cut a vertical slice through it at line A-A1(Fig1).
Now look at the cross section formed(Fig2).
Is it possible to calculate the volume of the original Torus? Prove your results.
The answer is yes. (The approximate volume is 18606 cubic millimeters)
Here's what I did: (This is really hard to explain)
Consider the plane perpendicular to A-A1 whose cross section is a circle of diameter 12.
Use to pythagorean theorem to find the distance from the outer edge of this circle to the point where plane A-A1 cuts it. This distance is 6 + sqrt(35). [35 = 6^2 - 1^2]
Consider a top view of this torus.
There is a right triangle (actually two) formed by the two plane sections and the points where they intersect the major diameter of the torus.
The legs of this triangle are 25 and 6+sqrt(35). Use the inverse-tangent to find the larger acute angle. It is about 64.5155 degrees.
Connect the ends of the hypotenuse to the center of the torus to form a isoceles triangle with its vertex at the center. This vertex angle can be found by 180 - 2*64.5155 = 50.967
There is also a right triangle with leg = 25 and angle = 50.967. The hypotenuse of this triangle is the outer radius (R) of the torus. Use sin(50.967) = 25/R to find R = 32.183
r = R - 12 = 20.183
V = .25*pi^2(R+r)(R-r)^2 = 18606.01786
[corrected volume formula] [twice]
Exact R = 25/(sin(180-2arctan(25/(6+sqrt(35)))))
Edited on December 2, 2004, 6:11 pm
Edited on December 2, 2004, 8:09 pm
|
|
Posted by Jer
on 2004-12-02 18:05:24 |



