Another ghost has trespassed into your haunted mansion. You are able to force him out, but only once you've caught up to him.
Both you and the other ghost take turns. During your turn, you may either stay in the same room, or move through a wall ceiling or floor to an adjacent room within the mansion (no moving diagonally). The other ghost does the same. You can sense each other's positions. The other ghost chooses the starting positions.
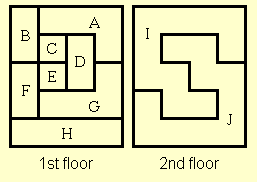
Given the above map of the mansion, can you catch the trespasser, or can he evade you indefinitely? Show a way to figure out the outcome of any given mansion.
The other ghost "prey" can be caught.
Create a connectivity matrix
A B C D E F G H I J
A * * * * * *
B * * * * *
C * * * * * *
D * * * * * *
E * * * * * *
F * * * * * * *
G * * * * * * * *
H * * * *
I * * * * * * *
J * * * * * * *
Now use that to show safe avenues for the prey.
If there exists a prey option that the predator does not have, then it is safe.
safe = and(prey options,xor(pred options,prey options)
X = no safe avenue, * = many, letter = only one
prey
A B C D E F G H I J
A x F * * * *
B * x * * *
C * * x G * *
D I B x * * *
E * * x * * *
F * * x * x A *
G * C C B x x B C
H * * x *
I * C * H * H x *
J * * * * x * x
So obviously, the prey can be trapped in H with the predator in F, G, or J. So the prey does not want to move to H if the predator can get to F, G, or H. This makes the chart look like.
prey
A B C D E F G H I J
A x F * * * *
B * x * * *
C * * x G * *
D I B x * * F *
E * * x * * J *
F * * x * x A *
G * C C B x x B C
H * * x *
I * C * x D x x *
J * * * * x * x
Continuing, we see now that the prey does not want to move to F if the predator can reach I, and I is reachable from F, G, or J.
prey
A B C D E F G H I J
A x x * * * *
B * x * * *
C * * x G * *
D I B x * * F *
E * * x * * J *
F * * x * x A *
G * C C B x x B C
H * * x *
I * C * x D x x *
J * * * * x * x
Continuing, we see now that the prey does not want to move to B if the predator can reach A, and A is reachable from I.
prey
A B C D E F G H I J
A x x * * * *
B * x * * *
C * * x G * *
D I x x * * F *
E * * x * * J *
F * * x * x A *
G C C C C C x x x x C
H * * x *
I * C * x D x x *
J * * * * x * x
Continuing, we see now that the prey does not want to move to C if the predator can reach D, and D is reachable from A. Note also that D is reachable from G and that there is nowhere left for the prey to go other than C if the predator is on G.
The prey is always catchable, the predator just needs to get to G.
Pred Prey
G H (Trapped)
Pred Prey
G J
G C
D B
A F
I H
J H (Trapped)
Pred Prey
G ABCDEFI
G B (or C, but see C above)
A F
I H
J H (Trapped)
This process can be applied for any mansion.
Edited on March 8, 2006, 5:18 pm




