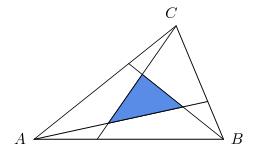
In triangle ABC, lines are drawn from the vertices to the first trisection points of the opposite sides, forming an internal triangle. What is the ratio of the area of the internal triangle to triangle ABC?

First I found the ratios into which the line segments were split by each other.  I used coordinate geometry but will leave out the details.  The ratio is 3:3:1.

Call the points on segments AB, BC and AC, by D, E and F.
Call the intersection of AE and CD by X
Call the intersection of AE and BF by Y
Call the intersection of BF and CD by Z

Let the area of triangle ABC = 1 square unit.

Consider triangle DBZ in comparison to ABC,
Its base DB is 2/3 as long as AB and
its height is 4/7 as high (because of the established ratio.)
Its area therefore is 1 * 2/3 * 4/7 = 8/21 square unit.

Now consider triangle XYZ in comparison to DBZ
Its base XZ is 3/4 of DZ and
its height is 1/2 as high.
Its area therefore is 8/21 * 3/4 * 1/2 = 1/7

So the area of the internal triangle is 1/7 as large as the external one.

 

Posted by Jer on 2007-02-02 12:40:39