Consider the 4 framed "gyroscopic" lattice in the top diagram along with its description to be a visual abstraction of something that could be embedded in an electronic device (like a graphics calculator).

Assume that each rotation can be programmed with a function having a forward or backward value, and that the effect of such an operation can be monitored on its central panel.

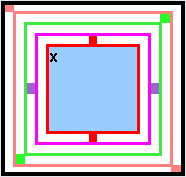
The axial rotations available are: - [V] vertical [red] - [H] horizontal [magenta] - [R] right-down diagonal [green] - [L] left-down diagonal [salmon] The smallest squares are the axial pivots.

Let these general functions be incorporated into an "x*y" array of LEDs.

On this occasion each LED is programmed to represent the axial reflection of its currently held image after being "flipped" ... but then ... the image is rotated 45° clockwise immediately.

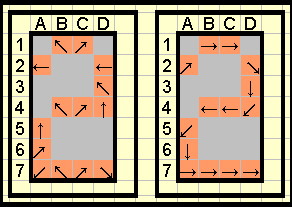
The numeral "2" has been 'scrambled' by the device in a 4*7 display at the left. What set of operations, per individual cell, is needed to produce the outcome at the right? The arrows are to represent the direction of writing the digit. For cell A2, "[L]" would produce the desired end result. The rotation would face the image upwards and then a 45° clockwise rotation would occur.