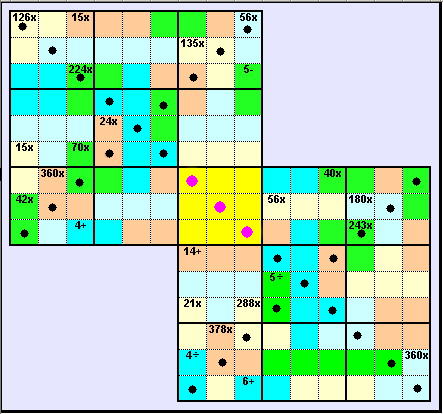
Place the numbers 1 to 9 once in each row, column, long diagonal and 3x3 box. Obviously, the central yellow-coloured 3x3 box is common to both grids.

The number in the cage (or shaded area) represents the result of an arithmetical operation by its accompanying sign. For example, 4÷ in a two-celled cage means that it contains either 8 and 2 or 4 and 1 (in any order).

Unlike Killer Sudoku, the same number may appear more than once in a cage. So, 28x in a cage which overlaps the 3x3 grids may contain two 2s and a 7.

Once again, I wish to thank brianjn most sincerely for his continued support. He converted my black and white Excel image to a coloured one in 'jpg' format.
Acknowledgement to Peter at sudexel.com for beta testing the puzzle.

(In reply to Request for additional numbers... by Dej Mar)

Dear Dej Mar,

Please be assured that I checked this about six times, before posting it. I admit that it is difficult, but the solution is unique. Two people on another site confirm its uniqueness.

The overlap cannot be solved using the top grid alone. It is necessary to refer to both 9x9 grids. As you say, the 7 cannot appear in r9c7 because of the 21x constraint.

I am going to send you an email which contains the solution to the overlap. Have a look if you wish! As soon as I can, I'll check it again and let you know.

Thanks for your interest.

:) Josie

Posted by Josie Faulkner on 2008-06-23 06:09:26