Modern mathematics has proved it impossible, but here is a simple and ingenious mathematical cardboard device that trisects accurately:
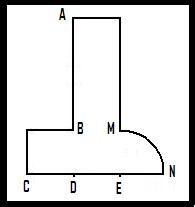
If you place it properly, so the edge AB passes through the vertex of the given angle, one side of the angle passes through point C, and the other side tangents the arc MN (arc of the circumference centered at E and radius ED), the lines traced from the vertex through the points D and E trisect exactly the angle.
Prove it.
The device is perfectly drawn to scale, so you can get any information you need about lengths, parallelism, intersections etc...



