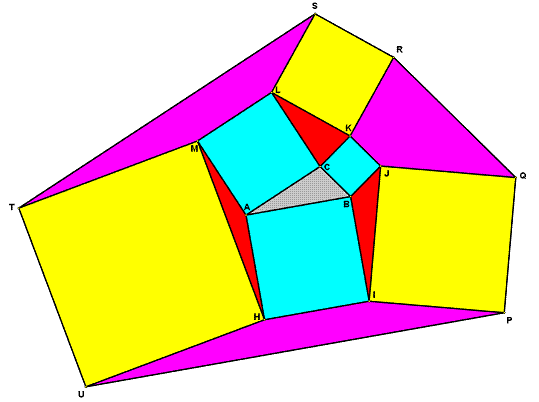
For the arbitrary triangle ABC in the figure below, prove that:

   1) The yellow area is three times the cyan area.

   2) The magenta area is five times the red area.

Note: The yellow and cyan areas are squares.

(In reply to yellow/cyan proof by Daniel)

Building on your proof.  Finding the Magenta areas requires finding the area of a quadrilateral when 3 sides and the two enclosed angles are known (SASAS).  I attempted to derive a formula for this.

Let the sides be a, b, and c with angle X between a and b and angle Y between b and c.

Area = .5(ab(sin(X))-bc(sin(Y))+ac(sin(Y-X))

this formula does not seem to work though so we cant use it to continue.

Posted by Jer on 2009-06-17 14:23:39