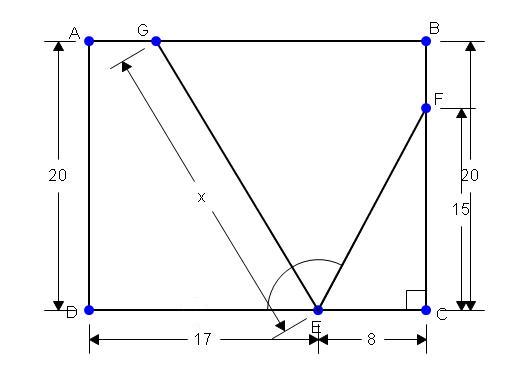
EF is 17 by pythagorean theorem
angle FEC is arccos(8/17)
angle GED is (180 - arccos(8/17))/2 = 90 - arccos(8/17)/2
construct a perpendicular to CD through G. Call the intersection H.
GH = 20
sin(90-arccos(8/17)/2)) = 20/x
x = 20/sin(90-arccos(8/17)/2))
=20/cos(arccos(8/17)/2))
by the half angle identity
=20/sqrt((cos(arccos(8/17))+1)/2
=20/sqrt(25/34)
=20*sqrt(34)/sqrt(25)
=4*sqrt(34) ≈23.32380758
|
|
Posted by Jer
on 2010-11-08 14:57:42 |