Begin with an arbitrary, convex quadrilateral. Next, draw squares outwardly on the sides of the quadrilateral, and join the centers of opposite squares.

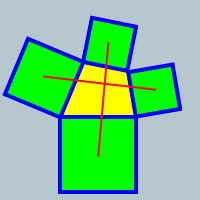
You might find the the two resulting lines are equal in length and intersect at precisely 90 degrees.

Prove (or disprove) the notion, that this is always true.

It sounds like they are expected to always intersect. It's quite esy to draw an example where they don't intersect though - make the quadrilateral a very wide-based, yet short, triangle with the top shaved off. The horizontal line will be formed above the top square.

However, I assume that you just mean the lines would be perpendicular were they to be extended.

I wonder if someone can provide us with a more intuitive proof then the one Federico linked?

Posted by Sam on 2004-01-10 11:18:21