Begin with an arbitrary, convex quadrilateral. Next, draw squares outwardly on the sides of the quadrilateral, and join the centers of opposite squares.

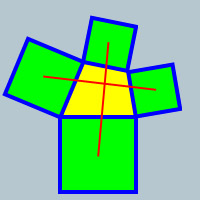
You might find the the two resulting lines are equal in length and intersect at precisely 90 degrees.

Prove (or disprove) the notion, that this is always true.

(In reply to Proof by Federico Kereki)

It's interesting that you used the work of a famous mathematician to solve this one. Just the other day, CNN announced that another noted mathematician, a Russian named Grigori Perelman, now has a definite answer for "Poincare's Conjecture", which ranks right up there with "Fermat's Last Theorem" among famous unsolved (until recently) mathematical problems. Perelman stands to get a cool million dollars for his achievement, although I'm sure he was motivated by a love of pure mathematics rather than a desire for monetary gain. Details of Perelman's coup can be found at:

http://www.theage.com.au/articles/2003/08/02/1059480600718.html
Edited on January 10, 2004, 12:45 pm

Posted by Penny on 2004-01-10 12:42:02