Begin with an arbitrary, convex quadrilateral. Next, draw squares outwardly on the sides of the quadrilateral, and join the centers of opposite squares.
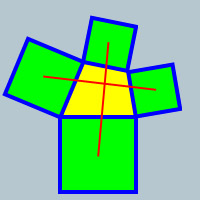
You might find the the two resulting lines are equal in length and intersect at precisely 90 degrees.
Prove (or disprove) the notion, that this is always true.
(In reply to
re: Small problem by TomM)
For what it's worth, I was looking for a "simpler" solution that didn't involve complex numbers. (When I say "simpler", I mean using real numbers only.) What Federico submitted is a valid solution, but certainly, not everyone in Flooble's audience is familiar with imaginary numbers and rotating complex vectors by multiplication of -i.
That being said, here's a nice link to an applet that helps explain this, and perhaps someone may choose to submit a different (perhaps Cartesian) solution.
re(2): Small problem
