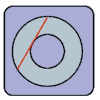
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.
We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.
What is the area (shaded in light-blue) between the two circles?
Rather than quote some rule, how about we prove it's true?
Equations to use:
Eq for Circle1 (inner):
x1^2 + y1^2 = r1 ^ 2
Eq for Circle2 (outer):
x2^2 + y2^2 = r2 ^ 2
Eq for Area between circles:
A = pi * r2^2 - pi * r1^2
Since the chord is tangent to Circle1, we know that the distance along the chord from the point it touches Circle1 to the point that it intersects Circle2 = 10/2 = 5 (radius' of both circles are perpendicular bisectors).
Establish a point on Circle2, using known x and y values:
Let x2 = r1
And we know y2 = 5 at that point, so now we have:
x2^2 + y2^2 = r2^2
r1^2 + 25 = r2^2
Substitute this into the Area equation:
A = pi * r2^2 - pi * r1^2
A = pi * (r1^2 + 25) - pi * r1^2
A = pi * r1^2 - pi * r1^2 + 25 * pi
A = 25 * pi
Voila
 Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.



