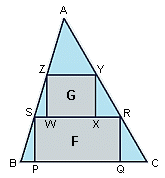
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.
What is the maximum total area of F and G?
For this I needed to add some figures into the picture, I called the line BC = 10cm, dropping a perpendicular line from A to an intersection of BC, say A-A', i called this length 10cm also,
this gives us an area for the triangle of 50cm², (base x 1/2 height)
now i need to insert 2 squares into the triangle, i used the equation ½height x ½width (5cm x 5cm) for the first (F) and ¼height x ¼width (2.5cm x 2.5cm) for the second (G)
from this i can now work out area of F+G to be 25cm²+6.25cm²=31.25cm²
this is 62.5% of the original triangles area
|
|
Posted by Juggler
on 2004-03-03 02:07:02 |



