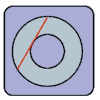
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.
We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.
What is the area (shaded in light-blue) between the two circles?
Ri - inner radius
Ro - outer radius
A - Area we're looking for
The Area of the light blue section is the difference between the area of the two circles, or....
A = pi( Ro^2 - Ri^2)
Using the tangent line we can create a triangle with vertices of the intersection of tangent line and the inner circle, one intersection of the outer circle and the tangent line, and the center of the circles. This creates a right triangle with sides of length Ri, Ro, and a hypotenuse of length 5 (the 10-in tangent line is bisected by at the intersection point of the inner circle - they are concentric).
So, using the Pythagorean theorem...
c^2 = a^2 + b^2
Ro^2 = Ri^2 + 5^2
Ri^2 = Ro^2 - 25
And substituting into the area equation above...
A = pi(Ro^2 - (Ro^2 - 25))
A = pi(Ro^2 - Ro^2 + 25)
A = 25*pi
solution
