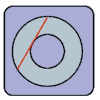
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.

We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.

What is the area (shaded in light-blue) between the two circles?

Assume the inner circle has radius 0 (since we don't know it, we can pick one that simplifies the math). Since a line tangential to that inner circle is the same as the radius of the outer circle, that makes the question into, "find the area of a circle with diameter 10." pi r^2, so the answer is 25*pi

Posted by narcoleptic on 2002-05-08 14:34:24