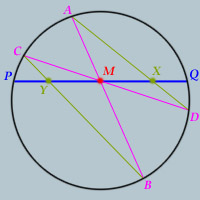
Given a circle and two points on that circle,
P and
Q, draw the chord
PQ, and label its midpoint
M.
Now draw two other chords of the circle AB and CD that both pass through M.
Further, draw chords AD and BC.
Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________
Prove that M is the midpoint of line segment XY.
(In reply to
Let's prove its converse. by Victor Zapana)
Given: An arbitrary circle
Chord PQ, with M as its midpoint
X and Y, such that P-Y-M-X-Q, and YM doesn not equal MX.
Prove: There can be no chords CB and AD, s.t. C-M-D, A-M-B, C-Y-B, and A-X-D at the same time.
Bear in mind, that chords CB and AD must be different, so neither chord can be chord PQ.
Proof: Create an arbitrary chord AD that intersects chord PQ at point X. Thus, A-X-D, for X is in the interior of the circle. This is because P-Y-M-X-Q, and PQ is a chord. Create a chord CD, s.t. C-M-D. Create a chord CB, s.t. C-Y-B. Create line segment AB, which is coincidentally chord AB.
Prove now: M is not on line segment AB.
[To Be Continued
re: Let's prove its converse.
