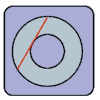
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.

We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.

What is the area (shaded in light-blue) between the two circles?

given:
(bigger) circle of radius R
(smaller) circle of radius r
a chord of length 10, tangent to the smaller circle

draw a diameter (perpendicular to the chord)
you will see that this can be broken into segments of length (R-r) and (R+r).
Recall formula that products of segments of 2 intersecting chords are equal in a circle

therefore: R^2-r^2 = 25
and we are looking for (R^2-r^2)*pi
so the area in between is 25 pi

Posted by Daniel on 2002-10-15 21:14:43