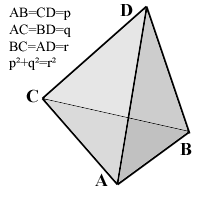
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with

AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².

What's its volume, as a function of p, q and r?

(In reply to Solution by Victor Zapana)

Going through the posted solution I see the first mistake in the first solution is the assumption that because angle DBA is a right angle, that the two planes meeting there (and all along line BC) are also perpendicular.  This is not the case. It would be the case only if angle CBA were also right, which it is not.  And in fact the angles are such that there is no height at all: it is zero.  Triangle CDB is coplanar with triangle CBA.

Posted by Charlie on 2004-04-27 09:18:39