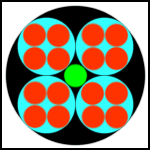
Begin with one
BLACK circle, and inscribe 4 identical, interior, cyclically tangent,
CYAN circles, such that they are also tangent to the black circle.
In each of the four cyan circles, inscribe 4 RED interior circles in exactly the same way.
Finally, inscribe a small GREEN circle in the center of the original black circle, tangent to the cyan circles.
Which is larger, this small green circle, or one of the small red circles?
Form a square such that its vertices are the centre of one of the CYAN circles, two tangent points and the centre of the GREEN circle.
<br>
The square contains a CYAN quadrant and a GREEN quadrant whose centres are the endpoints of a diagonal of the square (so formed).<br>
A RED circle within the CYAN quadrant has two sides of the square as tangents.<br>
Let the RADius of the RED circle be 1 unit.<br>
Let the RADIUS of the CYAN circle be C.<br>
Let the RADIUS of the GREEN circle be G.<br>
Let the Diagonal of the square be D.
<br>
The distance from the centre of the CYAN circle to centre of the RED circle is ¡î2 units.<br>
RADIUS C equals that distance + Radius Red, ie, ¡î2 +1 units.<br>
DIAGONAL D = /¡î(2*C©÷) = c¡î2<br>
RADIUS G = D - C<br>
= (¡î2+1).¡î2 - (¡î2+1)<br>
= (¡î2+1)(¡î2-1)<br>
= 1<br>
Radius of Green = Radius of Red.<br>
Both are the same.
|
|
Posted by brianjn
on 2004-06-17 08:34:39 |
Color Blindness
