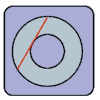
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.

We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.

What is the area (shaded in light-blue) between the two circles?

Narcoleptic's and Tom's (the other Tom) solutions are elegant, but they rely on the (unproven but true) assumption that the area is a constant , rather than a function of the two radii.

The relevant equations are:
A(C) = pi(R^2)
A(c) = pi(r^2)
A(C-c) = pi[(R^2)-(r^2)]
and
(r^2) + (5^2) = (R^2), which can be re-stated as (R^2)-(r^2) = (5^2) =25, and plugged into the third equation to produce:
A(C-c) = pi[25] = 25pi

Posted by TomM on 2002-05-09 23:34:50