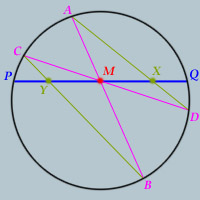
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.

Now draw two other chords of the circle AB and CD that both pass through M.

Further, draw chords AD and BC.

Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________

Prove that M is the midpoint of line segment XY.

(In reply to Too Simplistic? by brianjn)

Just because it's true for the two extremes does not prove it's true in the middle. Consider 1/(x^2+1). It approaches 0 as x goes to +/- infinity. But it is not 0 at any point in the middle.

Posted by np_rt on 2004-07-10 21:37:43