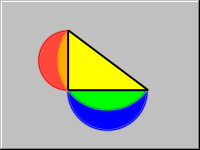
Given a right triangle, draw the three following semicircles:
- The semicircle with diameter formed by one of the legs and extending away from the triangle.
- The semicircle with diameter formed by the other leg and extending away from the triangle.
- The semicircle with diameter formed by the hypotenuse and extending towards the triangle.
Prove that the area of the two crescents (shown in RED and BLUE) formed by the three semicircles equals the area of the triangle.
The area of the two crescents (A) is (red semicircle) + (blue semicircle) + triangle – (hypotenuse semicircle) = A. So if I call the diameter of the red semicircle R, the diameter of the blue semicircle B, and the diameter of the hypotenuse semicircle H, here is what I get:
R^2 + B^2 = H^2 (Pythagorean theorem of the right triangle)
Red semicircle = 1/2*pi*(R/2)^2 = pi/8*R^2
Blue semicircle = pi/8*B^2
Hypotenuse semicircle = pi/8*H^2
A = pi/8*R^2 + pi/8*B^2 + triangle – pi/8*H^2 = pi/8*(R^2 +B^2 – H^2) + triangle = pi/8*(H^2 – H^2) + triangle = triangle.
So A = triangle
|
|
Posted by nikki
on 2004-08-11 09:42:35 |
 Given a right triangle, draw the three following semicircles:
Given a right triangle, draw the three following semicircles:


