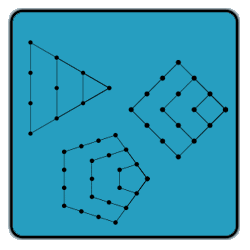
For starters, I will explain that a triangle number is any number X, such that if X dots were aranged in a a shape the first row would have one dot, the second two dots, the third three and so on, forming a triangular shape.

The first few triangle numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120. In other words you start by adding one, then two then, three etc. The formula for these is (n(n+1))/2.

Next square numbers which we learn as N squared. But they can also be expressed as ((n(n+1))/2) + ((n(n-1))/2). Here the first few are: 1, 4 ,9 ,16, 25, 36, 49. In this case, instaed of adding 1 then 2 then 3 you add 1 then 3 then 5 then 7 (i.e. every other number).

Next are pentagonal numbers which are also comprised of dots where the Nth pentagonal number is the number of dots in the figure. The first few are: 1, 5, 12, 22, 35, 51. Notice how first you add 1 then 4 then 7 then 10 then 13 (i.e. every third number). The formula is ((n(n+1))/2) + ((2)(n(n-1))/2).

Can you find a pattern in N-gons and prove it?

(using the previous notation)
The general formula is:

F(m, n) = n/2 * (mn - 2n - m + 4)

To prove:

Let F(m, n) = m(1) + m(2) + .. + m(n)
(eg: F(3, 4) = t(1)+t(2)+t(3)+t(4) = 1+2+3+4)
m(1) = 1, and m(n) = 1 + (m-2)(n-1)

pairing symmetrical terms:

m(1) + .. + m(n) = n/2 * (m(1) + m(n)) =
n/2 * (1 + 1 + (m-2)(n-1)) =
n/2 * (2 + mn - m -2n + 2) = the above

The case of n odd requires a slight modification,
you pair up n-1 terms plus central term
(m(central) = 1 + (m-2)(n-1/2)), but
it works out.

Posted by Cheradenine on 2002-12-02 00:43:36