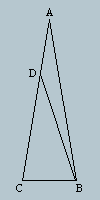
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
D is a point on side AC with AD=BC. Find angle DBC.
Solve this without trigonometry.
The tangent of angle DBC is [cos(10)/sin(10)]*[(1-2*sin(10))/(1+2*sin(10))] and my calculator says that this is the tangent of 70 degrees. Supposing then that this is exact, then angle ABD is 10 degrees, and if the perpendicular bisector of BC is erected, it will intersect DB at the point E such that AE=BE. This is enough on which to base a construction that, with enough perseverence, I hope can provide a non-trig solution.
The idea is to start with a circle, which will be the circumcircle of ABC, as the starting point of the construction. Given a circle, divide its circumference into 9 equal arcs. Triangle ABC is constructed by having BC be the line that connects the endpoints of one these arcs and has AC and AB joining the ends of BC to the appropriate intersection of the circle with the perpendicular bisector of BC. Call the center of the circle E. Draw the line through E and B which will intersect AC at what we will call D (and wish to show is the D of the problem). AE=EB and angle DBA is 10 degrees.
The perpendicular bisector of AC passes through E and will serve as an axis of symmetry about which some further construction paerhaps may establish that AD=BC. This further construction involves a copy of triangle ABC which will be called A'B'C'. A' will be C and B' will be A. C' will be the counterclockwise end of the arc that is 1/9 of the circumference of the circle and starts at B'. Let D' be the mirror image of D with respect to the axis of symmetry. We want to show that the triangle D'CB is isosceles with D'C=BC.
|
|
Posted by Richard
on 2004-09-08 12:37:36 |
 Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.


