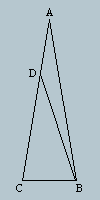
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
D is a point on side AC with AD=BC. Find angle DBC.
Solve this without trigonometry.
This is "cheating" but here is how I found the solution.
I had a really hard time going from what was purely given. However, in an attempt to brush up my geometric relationships, I was looking through the other Measure That Angle problems. I noticed a similarity with the first Measure That Angle problem. It also has AD = BC, and it turns out in the solution that angle A is also 20 degrees.
So I could say "place point E on AB such that AD = DE = EB = BC" which we know is possible (this is the cheat). Now we know that triangles ADE and DEB are isosceles. So angle DAE = angle DEA = 20 degrees. This means that angle DEB = 160 due to the Linear Pair Theorem.
Again, since triangle DEB is isosceles, and we know angle DEB = 160, we have 2*(angle DBE)+160 = 180. So angle DBE = 10.
Well, thatís all fine and dandy, but we wanted to know angle DBC. Well, angle ABC = 80 (since triangle ABC is isosceles and we know angle BAC = 20 degrees). So angle DBC + angle DBE = angle ABC, or angle DBC + 10 = 80.
So angle DBC = 70 degrees.
|
|
Posted by nikki
on 2004-09-08 12:44:58 |
 Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.


