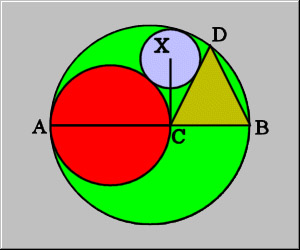
Consider a circle O with a diameter AB, shown here in green. Draw a second circle (red) with diameter AC, such that C is on AB. Draw an isosceles triangle with base CB and third vertex D on circle O. Draw a third circle (X), tangent to the first three figures. Prove that the line from C to the center of circle X is perpendicular to AB.

(In reply to re: First Step by Jim)

The biggest thing I wantd to find out was this...

making the diameter of the red circle and the base of the triangle splits the green circle in two. would this line split the blue circle?

numbers...I made the diameter of the green circle 100. this makes Ac and CB 50, making AF, FC, and FG 25. From prior post, CX is 2/3 50 = 33 1/3, making GX and HX 16 2/3. Add FG (25) to GX (16 2/3), FX = 41 2/3, making angle F 53.1 degrees.

Yes, all of this assumes CX is perpendicular to AB, but using the calculation, redraw the whole thing and see where the lines fall. It puts the blue circle tangent to the red circle, the triangle, and the outer circle, AND puts the center of the blue circle dead on the line from C to the top of the green circle. actually, finding the center of the blue circle on the line, then drawing it made the 3 tangent points exaclty where they should be.

Posted by Jim on 2004-09-09 12:16:41