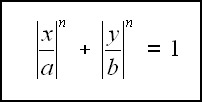There is a family of curves on the Cartesian plane described by this form:
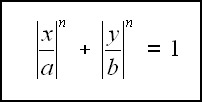
If n is equal to 2, then it describes an ellipse (if a = b, then it describes a circle).
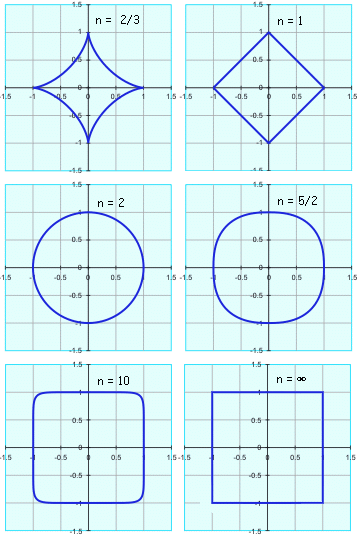
If n is greater than 2, then this is a "superellipse" (if a = b, then this is a supercircle).
As n increases, the ellipse becomes more "rectangularish", and as n approaches ∞, the limit is a rectangle (or a square if a=b).
What value must n have such that the figure has an area exactly halfway between the associated ellipse (when n=2) and rectangle (when n=∞)?
The graphs below, calculated by varying n with a = b = 1, show this property. Note that as n approaches zero, the curve degenerates into two crossed lines along the x- and y-axes.
In the simplest evaluation a=b=1 we have the area of a circle and the
area of a square, which when dealt with in the first quadrant is 1/4 of
the area. Integrating the equation across x:
Integral[(1-x^n)^(1/n) across x from 0 to 1]
When n = 2 (circle) the integral becomes pi/4 or 1/4 the area of a unit circle.
When n = infinity the integral becomes 1 or 1/4 of the area of the associated square (area = 4)
The area for the quarter section half way between would be (1-pi/4)/2 or 0.5-(pi/4)
Now solve the integral (probably numerically) for n such that...
Integral[(1-x^n)^(1/n) across x from 0 to 1] == 0.5-(pi/4)