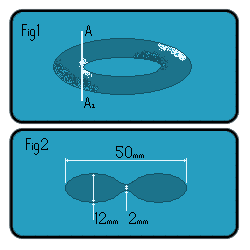
Take a regular torus (doughnut) shaped object and cut a vertical slice through it at line A-A1(Fig1).
Now look at the cross section formed(Fig2).
Is it possible to calculate the volume of the original Torus? Prove your results.
first, I am assuming that a regular torus is a circle of radius r
rotated about an axis with the center of the circle a distance R from
the axis.
From this assumption, the basic circle is known to have a height of 12,
therefore a radius of 6 (r = 6). The equation of the circle is
therfore (assuming this circle to be centered on an arbitrary x-y axis)
x^2+y^2=36. We know at a certain distance from the center of the
circle we have a point which y = 1 (for the vertical distance of
2). Solving at this point for x we get ±√35. The distance from
the center of the torus to this point on the x axis would be R-√35.
Now, creating an isoceles triangle with long length 50, height of
R-√35, and the two other legs of length R+r. Using pathag. we can
solve for R...25^2+(R-√35)^2=(R+r)^2
Solving for R I got ≈ 26.183
The volume of a torus is 2π^2r^2R ≈ 18606 mm^3
I think this is correct, a little hard to explain without pictures...
Edited on December 2, 2004, 7:25 pm



