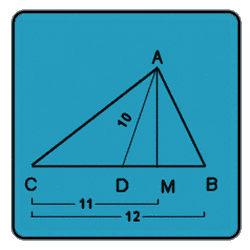
If ABC is a right triangle, the hypotnuse must always be larger then the length of either legs. SO for ABC:
BC>AC....
But BC=12 and the solution for AC is 14? This can't be true for a real triangle.
Another approach to the problem yields a different answer.
Triangles ABC and MAC are similar because:
angle BAC= angle AMC= 90
Angle BCA= Angle ACM
Therefore: (AC/CM)=(BC/AC) or AC^2=BC*CM
BC=12 and CM =11 so AC^2= 12*11=132
AC=sqrt132 =(approx) 11.5
Now, why don't both answers agree??????
|
|
Posted by B
on 2004-12-03 17:10:04 |