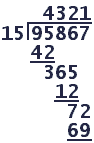The following long division problem is not correct. In fact, none of the digits is what it should be.

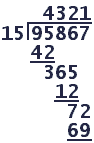
Change each of the digits to a different digit so that the arithmetic is correct.

Note that there is no remainder, no leading zeroes, and like digits are not necessarily all changed to the same digit.

From my previous posts, the divisor ranges from 23-33, excluding 25. And the quotient ranges of the form wxyz. w=1,2,3. x=0, y=3,4. z=2,3,4.

There are 10 values for the divisor and 18 values for the quotient giving a total of 180 possibilities. I couldn't further narrow it down so I took multiplied them all out.

After multiplying them out and using the following restrictions for the product, I narrowed it down to 8 possibilities

1. Ten-thousands digit is not 9.
2. Thousands digit is not 5.
3. Hundreds digit is 0.
4. Tens digit is not 5 or 6.
5. Units digit is not 7, 2, or 9.

That gives

24*2042=49008
24*3042=73008
30*1034=31020
30*2034=61020
31*1033=32023
31*2033=63023
32*1032=33024
32*1034=33088

The thousands digit in the quotient times the divisor cannot have a tens digit of 4 nor a ones digit of 2. That further drops it down to 3.

30*1034=31020
30*2034=61020
31*1033=32023

The last elimination is that the "12" in the 90's. It turns out that for a divisor of 30, it comes out exactly to be 90, which isn't enough.

That leaves 31*1033=32023.

Posted by np_rt on 2004-12-03 19:18:57