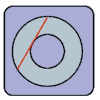
Consider the picture to the right. We have two concentric circles, one inside another. We do not know the radius for either one of them.
We do, however know that the chord (shown in red) - a line whose ends are on the outer circle and which is tangent to the inner circle - has a length of 10 inches.
What is the area (shaded in light-blue) between the two circles?
We drop a perpendicular from the centre to the point where the line is a tangent to the inner circle. Then we see that the perpendicular drawn is the radius of the smaller circle and the line joining the centre to the point where the tangent to the smaller circle meets the larger circle is nothing but the radius of the larger circle. Hence by using Pythagoras Theorem for the right angled triangle thus formed, we see that the difference between the squares of the radii of the larger circle to that of the smaller circle is equal to the square of half the length of the line (in red) drawn in the picture. Thus the required area will be equal to 50(pi), where 'pi' is the ratio of the circumference to the diameter and its value is (22/7). Thus the required area is : 157.142857 (approximately) square inches.
What's the Area ?
