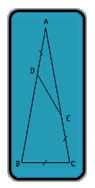
Sorry, couldn't resist posting this solution, which avoids flipping.
Let a be the measure of angle BAC and let d be the length of AD. Draw CF with F inside ─ABC, angle FCE equal to a, and FC of length d. Then FC is parallel to DE because both make the same angle with AC. Since FC and DE are parallel lines of the same length, DECF is a parallelogram. So DF has length d and angle FDE equals a. Now here's the sneaky part.
A, E, and F all lie on a circle of radius d centered at D. Since angle FDE equals a, it follows, by the half-angle formula for chords of a circle, that angle FAE equals a/2. Thus AF is coincident with the bisector of angle BAC, which is also the perpendicular bisector of BC (because ─ABC is isosceles). But then BF has length d because F is on the perpendicular bisector of BC and CF has length d. Thus ─BFC is equilateral with its 60 degree angles equal that of BCF, which is
60 = angle BCF = angle BCE - a = (180-a)/2 - a =90 - 3a/2.
(angle BCE=(180-a)/2 because ─ABC is isosceles) Solving this equation for a yields a=20 degrees.
|
|
Posted by McWorter
on 2005-03-07 03:34:32 |
 Given that:
Given that:


