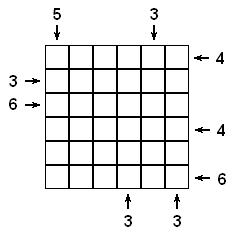
Every square in the diagram below has a building of between 1 and 6 stories, inclusive.

No two buildings in any row or column have the same number of stories. Also, on one of the diagonals, no two buildings have the same number of stories, though the other diagonal has a repeat.

The numbers around the perimeter indicate the number of buildings visible when looking in the direction indicated by the arrow. Note that shorter buildings are not visible if they are behind a taller building. Determine the height of building on each square.

This puzzle was inspired by a puzzle on the Google Puzzle practice exam.

Number the columns from 1-6 and rows A-F.

Start with the rows & columns where you can see all 6 buildings as they have to be in ascending order:

+--+--+--+--+--+--+
 l    l    l    l    l    l    l
+--+--+--+--+--+--+
 l    l    l    l    l    l    l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l    l    l    l    l    l    l
+--+--+--+--+--+--+
 l    l    l    l    l    l    l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

Column 1 has 5 buildings visible so you know that the 4 spaces will be 2, 3, 4 & 5

+--+--+--+--+--+--+
 l 2 l    l    l    l    l    l
+--+--+--+--+--+--+
 l 3 l    l    l    l    l    l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l    l    l    l    l    l
+--+--+--+--+--+--+
 l 5 l    l    l    l    l    l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

Square A6 will be either a 3, 4 or 5 but because you have to see 4 buildings it can't be a 4 or 5 so must be a 3. Similarly D6 must be a 2. From this you can then deduce the other two spaces in column 6 must be 4 & 5, E6 can't be a 5 so must be 4 leaving B6 as 5:

+--+--+--+--+--+--+
 l 2 l    l    l    l    l 3 l
+--+--+--+--+--+--+
 l 3 l    l    l    l    l 5 l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l    l    l    l    l 2 l
+--+--+--+--+--+--+
 l 5 l    l    l    l    l 4 l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

The 6 in column 4 can't be in squares D4 and E4 because then you wouldn't see 3 buildings up that column, also it can't be in A4 as you wouldn't see 4 buildings from right to left in row A therefore B4 must be 6. By similar deductionsif where 6 can't go in column 5 square E5 must be 6 also:

+--+--+--+--+--+--+
 l 2 l    l    l    l    l 3 l
+--+--+--+--+--+--+
 l 3 l    l    l 6 l    l 5 l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l    l    l    l    l 2 l
+--+--+--+--+--+--+
 l 5 l    l    l    l 6 l 4 l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

In column 5 a 3 can't go in A5 or B5 therefore it must be in D5. in row B a 2 can't go in B2 or B5 therefore it must be in B3. Square E3 can't be a 2,3,4,5 or 6 therefore it must be a 1. The other 2 squares in row E are 2 and 3, with 3 in E2 and 2 in E4

+--+--+--+--+--+--+
 l 2 l    l    l    l    l 3 l
+--+--+--+--+--+--+
 l 3 l    l 2 l 6 l    l 5 l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l    l    l    l 3 l 2 l
+--+--+--+--+--+--+
 l 5 l 3 l 1 l  2 l 6 l 4 l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

if you now look at the diagonals, the one from A6 to F1 has a duplicate of 3 therefore the diagonal A1 to F6 must have no repeats so from this you can deduce that B2 is 4 and D4 is a 5. B5 must then be a 1, A4 a 1, A5 a 4:

+--+--+--+--+--+--+
 l 2 l    l    l 1 l  4 l 3 l
+--+--+--+--+--+--+
 l 3 l 4 l 2 l  6 l 1 l 5 l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l    l    l 5 l 3 l 2 l
+--+--+--+--+--+--+
 l 5 l 3 l 1 l  2 l 6 l 4 l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

Then A2 is a 6, A3 a 5. D2 a 1 and D3 a 6. You can then check the numbers around the grid to see if the number of buildings you can see matches.

+--+--+--+--+--+--+
 l 2 l 6 l 5 l  1 l  4 l 3 l
+--+--+--+--+--+--+
 l 3 l 4 l 2 l  6 l 1 l 5 l
+--+--+--+--+--+--+
 l 1 l 2 l 3 l  4 l 5 l 6 l
+--+--+--+--+--+--+
 l 4 l 1 l 6 l  5 l 3 l 2 l
+--+--+--+--+--+--+
 l 5 l 3 l 1 l  2 l 6 l 4 l
+--+--+--+--+--+--+
 l 6 l 5 l 4 l  3 l 2 l 1 l
+--+--+--+--+--+--+

I like Percy think there are 2 repeats on 1 diagonal

Posted by Lisa on 2005-09-07 09:26:21