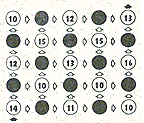
If traveling through a white circle takes that many minutes, and black circles represent backwards jumps in time that save 5 minutes, what's the shortest trip through this map?

From the spanish MENSA site.

(In reply to try this by Goldwing)

Well, just because it's a mensa problem doesn't say much about its difficulty.  In my experience, mensa puzzles aren't always good quality, though that's just my personal opinion.



For kicks, my solution:

Since all arrows point right or up, we can separate the map into 9 diagonals.  We must always move from diagonal 1 to diagonal 2 to 3, etc.  Every even numbered diagonal, no matter where we land, we go back 5 minutes.  Therefore, I will ignore these rows until it comes to final calculations.  Similarly, in all other diagonals, I will scale down the numbers so that the lowest number in each is 0.  For example, diagonal 3 would have numbers 2, 0, and 1.

  0
 201
05300
 034
  0

If you at all follow what I am doing (it went a lot faster in my mind than in this explanation), you know that I want to get from the top 0 to the bottom 0 while minimizing the sum of the numbers I pass.  The solution pretty clearly goes 0+2+0+0+0 = 2.

For final calculations, I add in all the minutes that I had first subtracted, and also go back in time a total of 20 minutes.  The total comes to 41 minutes.

Posted by Tristan on 2005-10-12 04:20:36