Below is a grid of squares. You may recolor any of the white squares. Your goal is to recolor them such that all squares of any one color are connected in a single unbroken region. Squares do not connect diagonally to each other.

The twist: The board has the topology of a mobius strip. The numbers indicate that the right and left sides are connected in reverse order. For instance, the upper left cyan corner square and lower right blue corner square are directly connected.

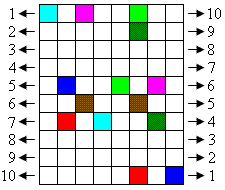
That was fun to work out Tristan.

I just realized I had an extra column in my solution grid.  My solution isn't valid.  See Hugo's post for the solution.

Edited on December 23, 2005, 12:50 am

Posted by MindRod on 2005-12-22 12:12:51