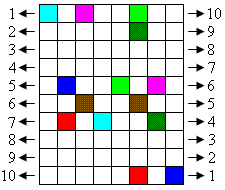
Below is a grid of squares. You may recolor any of the white squares. Your goal is to recolor them such that all squares of any one color are connected in a single unbroken region. Squares do not connect diagonally to each other.

The twist: The board has the topology of a mobius strip. The numbers indicate that the right and left sides are connected in reverse order. For instance, the upper left cyan corner square and lower right blue corner square are directly connected.

(In reply to My solution by Hugo)

"My solution, which is probably identical to Mindrod's."

NOPE! They are different.

Posted by Richard on 2005-12-22 15:42:35