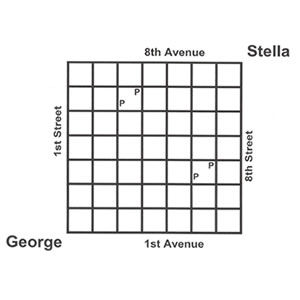
George lives at the corner of 1st Street and 1st Avenue. Each afternoon George visits his girlfriend, Stella, who lives at the corner of 8th Street and 8th Avenue. He varies his route but always walks 1400 meters (it is 100 meters between adjacent Streets and between adjacent Avenues). Sometimes he stops at one of the corner pubs marked as P in the diagram.

On May 1st 2006, after several months of these visits, Stella wants to get married and says to George, "If you don't propose marriage to me soon, I am going to propose to you." George replies, "Starting tomorrow I will walk a different route to your house and when I have used all the different possible routes, you can propose to me." "OK," says Stella, "but you must never go through an intersection with a pub at one of its corners." "It's a deal" replies George.

On what date will Stella be able to propose to George?

George when Stella proposes, remember that even before the marriage she told you to stay away from the pubs, so say NO.

As to the problem, I had a theory that said taht George had to take a decision at each corner so there where 2^12 possibilities, less the pubs. But looking at the problem a bit better, shot my nice theory down.

Edited on December 26, 2005, 2:28 pm

Posted by Hugo on 2005-12-26 10:15:38