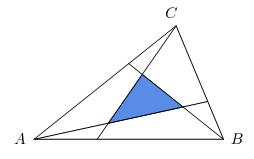
In triangle ABC, lines are drawn from the vertices to the first trisection points of the opposite sides, forming an internal triangle. What is the ratio of the area of the internal triangle to triangle ABC?
Let <PQ> denote the vector from point P
to point Q and [IJK...N] denote the area
of polygon IJK...N. Let ABC be the triangle
and AA', BB', and CC' the cevians in
question. Let A* be the intersection of
AA' and CC', B* be the intersection of
BB' and AA', and C* be the intersection of
CC' and BB'.
<AA*> = x<AC'> + (1-x)<AC>
= x<AB>/3 + (1-x)<AC> (1)
<AA*> = <AC> + y<CA'> + (1-y)<CA>
= 2y<AB>/3 + y<AC>/3 (2)
Since <AB> and <AC> are independent
vectors, (1) and (2) imply
y = 3/7
and therefore by (2)
<AA*> = 2<AB>/7 + <AC>/7
We can find the area of triangles by
using the cross product of vectors
[ABC] = (1/2) |<AB> x <AC>|
[AC'A*] = (1/2) |<AC'> x <AA*>|
= (1/2) |<AB>/3 x (2<AB>/7 + <AC>/7)|
= (1/2) |(<AB> x <AC>)/21|
Therefore, [AC'A*] = [ABC]/21 and by symmetry,
[AC'A*] = [BA'B*] = [CB'C*]
Now we find the area of the quadrilaterals:
[ABA'] = [AC'A*] + [C'BB*A*] + [BA'B*]
= [C'BB*A*] + 2[ABC]/7 = [ABC]/3
Therefore, [C'BB*A*] = 5[ABC]/21 and by symmetry,
[C'BB*A*] = [A'CC*B*] = [B'AA*C*]
Now we find the area of the internal triangle:
[ABC] = [A*B*C*] + [AC'A*] + [BA'B*] + [CB'C*]
+ [C'BB*A*] + [A'CC*B*] + [B'AA*C*]
= [A*B*C*] + 3[ABC]/21 + 15[ABC]/21
Therefore, [A*B*C*] = [ABC]/7
Note: The areas above were verified by Geometer's Sketchpad.
|
|
Posted by Bractals
on 2007-02-02 12:15:06 |





