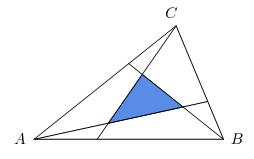
In triangle ABC, lines are drawn from the vertices to the first trisection points of the opposite sides, forming an internal triangle. What is the ratio of the area of the internal triangle to triangle ABC?
Without loss of generality, let the coordinates of triangle ABC be A(0,0), B(3a,0), and C(3c,3b). Let D,E, and F represent the trisection points on sides AB,BC, and CA respectively. The coordinates for these points are D(a,0), E(2a+c,b), and F(2c,2b). So the equations for the trisection segments are: y=bx/(2a+c) for AE, y=(2bx-6ab)/(2c-3a) for BF, and y=(3bx-3ab)/(3c-a) for CD. Let the vertices for the internal triangle be P,Q, and R (where P is the intersection of CD and AE, and Q is the intersection of AE and BF). By solving above equations simultaneously, we get coordinates P((3/7)(2a+c),3b/7), Q((6/7)(2a+c),6b/7), and R((3/7)(a+4c),12b/7). By evaluating a 3 by 3 determinant using these coordinates, the area of triangle PQR is 9ab/14. Since original triangle area is 9ab/2, the ratio of areas is 1/7.
|
|
Posted by Dennis
on 2007-02-02 12:56:54 |





