For some pieces and column widths it is trivial to see that an infinite game is possible. For example the I tetromino with any column width or any other of the tetrominoes with an even column width.
| For other pieces, an infinite game is possible, but not trivially so. Consider the T tetromino in three columns, an infinite game is possible by following a pattern: The first piece is horizontal with the stem of the T pointing down. The second piece is vertical, with the stem of the T pointing to the right and the T is pushed to the left edge. The third piece is vertical, with the stem of the T pointing to the left and the T is pushed to the right edge. |
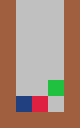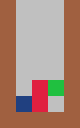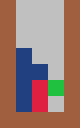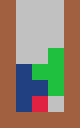
|
For each piece and number of columns listed below, find a strategy for each which allows for an infinite game:
1. 2.
### in three columns ### in four columns
# #
#
3. 4.
### in four columns ##### in five columns
# #
#
-----------------------------------------------------
Notes:
1 - Using the reflection of an asymmetrical piece is not allowed.
2 - Use classic gravity: when a row is filled, it is removed and all rows above move down, but no fragments of one partially filled row fall into another partially filled row.



