Three circles (A, B, and C) are tangentially connected:

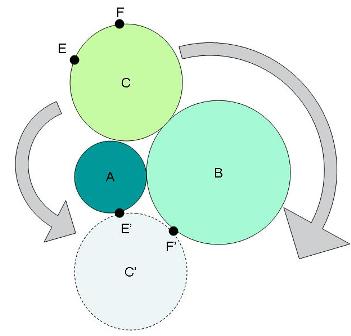
Properties:
1) Circle B's radius is twice the radius of Circle A.
2) Circle C is of the exact size that if it rolls around A, or it rolls around B, it will touch A and B on the opposite side at identical points E and F.

What is the radius of Circle C if:
1) C > B
2) B > C > A
3) A > C (C is a maximum)

(In reply to solution part 1 by Charlie)

I think the only modification needed for multiple rotations of C is to change 2*pi*x - 2*C*x to k*2*pi*x - 2*C*x, as the two portions skipped over remain without multiplication.

Only

needed = 2 * pi * x - 2 * c * x

need be changed, to, say

needed = 2 * 2 * pi * x - 2 * c * x

and the initial estimate of x changed.

This results in

 1.276999999999969  .0001 
 1.276999999999969  .00001 
 1.27704999999997   .000001 
 1.277054999999969  .0000001 
 1.27705589999997   .00000001 
 1.27705596999997   .000000001 
 1.27705597699997   .0000000001 
 1.27705597729997   .00000000001 
 1.27705597735997   .000000000001 
 1.277055977364971  .0000000000001 
 1.27705597736567   .00000000000001 
 1.27705597736575   .000000000000001 
 1.277055977365758  .0000000000000001 

indicating a radius of  1.277055977365758 relative to the radius of A for part 2.

With k = 3, we get

 .85                .001 
 .858               .0001 
 .8587999999999999  .00001 
 .8588599999999996  .000001 
 .8588619999999997  .0000001 
 .8588622999999995  .00000001 
 .8588623099999996  .000000001 
 .8588623099999996  .0000000001 
 .8588623103999996  .00000000001 
 .8588623104199996  .000000000001 
 .8588623104209996  .0000000000001 
 .8588623104213997  .00000000000001 
 .8588623104214597  .000000000000001 
 .8588623104214617  .0000000000000001 
 .8588623104214621  1D-17 

Indicating a radius of .8588623104214621 for C. This is the largest that is less than 1 (i.e., less than the radius of circle A).

For curiosity:

With k=4,

 .6                 .01 
 .64                .001 
 .648               .0001 
 .6488999999999999  .00001 
 .6489199999999998  .000001 
 .648927            .0000001 
 .6489276999999997  .00000001 
 .6489277900000001  .000000001 
 .648927794         .0000000001 
 .6489277945        .00000000001 
 .64892779453       .000000000001
 .6489277945349999  .0000000000001 
 .6489277945358002  .00000000000001 
 .6489277945358501  .000000000000001 
 .6489277945358561  .0000000000000001 
 .6489277945358563  1D-17 

indicating a radius of .6489277945358563 for circle C.

then

k=5

 .5  .01
 .52  .001
 .522  .0001
 .5224  .00001
 .5224199999999999  .000001
 .522424  .0000001
 .5224248999999995  .00000001
 .5224249499999998  .000000001
 .5224249519999997  .0000000001
 .5224249524999998  .00000000001
 .5224249525199998  .000000000001
 .5224249525259996  .0000000000001
 .5224249525261997  .00000000000001
 .5224249525262896  .000000000000001
 .5224249525262986  .0000000000000001
 .5224249525262988  1D-17

k=6

 .4  .01
 .43  .001
 .4370000000000001  .0001
 .4377  .00001
 .43773  .000001
 .437732  .0000001
 .4377325  .00000001
 .4377325899999999  .000000001
 .437732592  .0000000001
 .4377325925  .00000000001
 .43773259252  .000000000001
 .437732592521  .0000000000001
 .4377325925216998  .00000000000001
 .4377325925217498  .000000000000001
 .4377325925217498  .0000000000000001
 .4377325925217499  1D-17

k=7

 .3  .01
 .3700000000000001  .001
 .3760000000000001  .0001
 .3769  .00001
 .3769900000000001  .000001
 .376993  .0000001
 .3769939  .00000001
 .37699391  .000000001
 .3769939150000002  .0000000001
 .3769939152000002  .00000000001
 .3769939152100002  .000000000001
 .3769939152150001  .0000000000001
 .3769939152155  .00000000000001
 .3769939152155499  .000000000000001
 .3769939152155589  .0000000000000001
 .3769939152155598  1D-17

k=8 

.3  .01
 .3300000000000001  .001
 .3310000000000001  .0001
 .3312  .00001
 .3312600000000001  .000001
 .3312659999999999  .0000001
 .3312669  .00000001
 .33126693  .000000001
 .3312669380000002  .0000000001
 .3312669387000002  .00000000001
 .3312669387300002  .000000000001
 .3312669387370001  .0000000000001
 .3312669387375  .00000000000001
 .3312669387375799  .000000000000001
 .3312669387375869  .0000000000000001
 .3312669387375877  1D-17
 

k=9

.2  .01
 .2900000000000001  .001
 .2950000000000001  .0001
 .2955  .00001
 .2955700000000001  .000001
 .295575  .0000001
 .295575  .00000001
 .2955750699999999  .000000001
 .2955750760000001  .0000000001
 .2955750761000001  .00000000001
 .2955750761200001  .000000000001
 .295575076124  .0000000000001
 .2955750761243999  .00000000000001
 .2955750761244399  .000000000000001
 .2955750761244409  .0000000000000001
 .295575076124441  1D-17
 

k=10

.2  .01
 .2600000000000001  .001
 .2660000000000001  .0001
 .2669  .00001
 .26692  .000001
 .2669259999999998  .0000001
 .2669265999999998  .00000001
 .2669266599999998  .000000001
 .2669266619999999  .0000000001
 .2669266624999999  .00000000001
 .2669266625899999  .000000000001
 .2669266625929999  .0000000000001
 .2669266625930998  .00000000000001
 .2669266625931198  .000000000000001
 .2669266625931208  .0000000000000001
 .2669266625931216  1D-17

and, skipping, to k = 20

 .1  .01
 .13  .001
 .136  .0001
 .1364  .00001
 .13648  .000001
 .1364870000000001  .0000001
 .1364870000000001  .00000001
 .13648701  .000000001
 .136487012  .0000000001
 .1364870124000001  .00000000001
 .1364870124300001  .000000000001
 .1364870124390001  .0000000000001
 .1364870124392001  .00000000000001
 .1364870124392501  .000000000000001
 .1364870124392591  .0000000000000001
 .1364870124392594  1D-17

Posted by Charlie on 2007-12-27 21:01:17