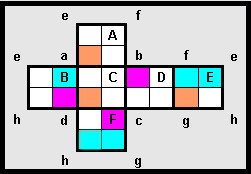
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
(In reply to
re(4): Clarifications?? by ed bottemiller)
You have two lists of square numbers, 3 digit and 4 digit from which you are working.
In the case of the 4 digit numbers clearly the 10³ digit is to appear in a coloured cell, and similarly with a 3 digit number the 10² digit will appear in a coloured cell which marks its starting point.
By "uniqueness" I am seeking for a specific square from your list to be used only once allowing for the fact that you may write the digits in clockwise or anticlockwise order; I see no difficulty in palindromes, I realise that 121 can be read as 112 if read in the opposite direction but I didn't want to make an issue it.
|
|
Posted by brianjn
on 2008-05-01 20:42:04 |




