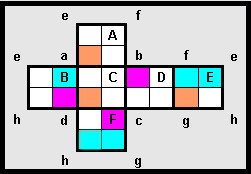
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
The program was not designed to eliminate multiple occurrences of the 3-digit vertex squares, as one duplication was allowed. Any more than the one duplication (the presence of fewer than 7 distinct 3-digit squares at vertices) was weeded out of the results by hand.
Dim sqr4(200), sqr3(100), had4(200), ctSol, numSqr3, vCt(100)
Private Sub cmdStart_Click()
Open "squares on cube.txt" For Output As #2
FontTransparent = False
For i = 100 To 999
sr = Int(Sqr(i) + 0.5)
If sr * sr = i Then
s = LTrim(Str(i))
If InStr(s, "0") = 0 Then
numSqr3 = numSqr3 + 1
sqr3(numSqr3) = s
Print s; " ";
End If
End If
Next
Print: Print numSqr3: Print
For i = 1000 To 9999
sr = Int(Sqr(i) + 0.5)
If sr * sr = i Then
s = LTrim(Str(i))
If InStr(s, "0") = 0 Then
numSqr4 = numSqr4 + 1
sqr4(numSqr4) = LTrim(Str(i))
Print s; " ";
End If
End If
Next
Print: Print numSqr4: Print
DoEvents
For A = 1 To numSqr4
CurrentX = 1: CurrentY = TextHeight("X") * 12
Print A; numSqr4; ctSol: DoEvents
had4(A) = True
Aa = Left(sqr4(A), 1)
For dirA = 1 To 2
If dirA = 1 Then
Ae = Mid(sqr4(A), 2, 1)
Af = Mid(sqr4(A), 3, 1)
Ab = Mid(sqr4(A), 4, 1)
Else
Ab = Mid(sqr4(A), 2, 1)
Af = Mid(sqr4(A), 3, 1)
Ae = Mid(sqr4(A), 4, 1)
End If
For va = 1 To numSqr3
vCt(va) = vCt(va) + 1
For dirVa = 1 To 2
goodVa = True
If Mid(sqr3(va), 2, 1) = Aa And dirVa = 1 Then
Ba = Left(sqr3(va), 1): Ca = Right(sqr3(va), 1)
ElseIf Mid(sqr3(va), 3, 1) = Aa And dirVa = 2 Then
Ba = Left(sqr3(va), 1): Ca = Mid(sqr3(va), 2, 1)
Else
goodVa = False
End If
If goodVa Then
For B = 1 To numSqr4
If had4(B) = False Then
For dirB = 1 To 2
goodB = True
If dirB = 1 And Mid(sqr4(B), 4, 1) = Ba Then
Bd = Left(sqr4(B), 1)
Bh = Mid(sqr4(B), 2, 1)
Be = Mid(sqr4(B), 3, 1)
ElseIf dirB = 2 And Mid(sqr4(B), 2, 1) = Ba Then
Bd = Left(sqr4(B), 1)
Bh = Mid(sqr4(B), 4, 1)
Be = Mid(sqr4(B), 3, 1)
Else
goodB = False
End If
If goodB Then
had4(B) = True
For vd = 1 To numSqr3
vCt(vd) = vCt(vd) + 1
If Left(sqr3(vd), 1) = Bd Then
For dirVd = 1 To 2
If dirVd = 1 Then
Cd = Mid(sqr3(vd), 2, 1)
Fd = Mid(sqr3(vd), 3, 1)
Else
Fd = Mid(sqr3(vd), 2, 1)
Cd = Mid(sqr3(vd), 3, 1)
End If
For C = 1 To numSqr4
If had4(C) = False Then
If Left(sqr4(C), 1) = Cd Then
For dirC = 1 To 2
goodC = True
If dirC = 1 And Mid(sqr4(C), 2, 1) = Ca Then
Cb = Mid(sqr4(C), 3, 1)
Cc = Mid(sqr4(C), 4, 1)
ElseIf dirC = 2 And Mid(sqr4(C), 4, 1) = Ca Then
Cb = Mid(sqr4(C), 3, 1)
Cc = Mid(sqr4(C), 2, 1)
Else
goodC = False
End If
If goodC Then
had4(C) = True
For vertb = 1 To numSqr3
vCt(vertb) = vCt(vertb) + 1
For dirVb = 1 To 2
If dirVb = 1 And Mid(sqr3(vertb), 2, 2) = (Cb & Ab) Or dirVb = 2 And Mid(sqr3(vertb), 2, 2) = Ab & Cb Then
Db = Left(sqr3(vertb), 1)
For D = 1 To numSqr4
If Left(sqr4(D), 1) = Db And had4(D) = False Then
For dirD = 1 To 2
If dirD = 1 Then
Df = Mid(sqr4(D), 2, 1)
Dg = Mid(sqr4(D), 3, 1)
Dc = Mid(sqr4(D), 4, 1)
ElseIf dirD = 2 Then
Df = Mid(sqr4(D), 4, 1)
Dg = Mid(sqr4(D), 3, 1)
Dc = Mid(sqr4(D), 2, 1)
End If
had4(D) = True
For vc = 1 To numSqr3
vCt(vc) = vCt(vc) + 1
For dirVc = 1 To 2
If dirVc = 1 And Mid(sqr3(vc), 2, 2) = (Cc & Dc) Or dirVc = 2 And Mid(sqr3(vc), 2, 2) = Dc & Cc Then
Fc = Left(sqr3(vc), 1)
For F = 1 To numSqr4
If Fc = Left(sqr4(F), 1) And had4(F) = False Then
had4(F) = True
For dirF = 1 To 2
goodF = True
If dirF = 1 And Fd = Mid(sqr4(F), 4, 1) Then
Fg = Mid(sqr4(F), 2, 1)
Fh = Mid(sqr4(F), 3, 1)
ElseIf dirF = 2 And Fd = Mid(sqr4(F), 2, 1) Then
Fg = Mid(sqr4(F), 4, 1)
Fh = Mid(sqr4(F), 3, 1)
Else
goodF = False
End If
If goodF Then
For vh = 1 To numSqr3
vCt(vh) = vCt(vh) + 1
If Fh = Left(sqr3(vh), 1) Then
For dirVh = 1 To 2
goodVh = True
If dirVh = 1 And Mid(sqr3(vh), 3, 1) = Bh Then
Eh = Mid(sqr3(vh), 2, 1)
ElseIf dirVh = 2 And Mid(sqr3(vh), 2, 1) = Bh Then
Eh = Mid(sqr3(vh), 3, 1)
Else
goodVh = False
End If
If goodVh Then
For vg = 1 To numSqr3
vCt(vg) = vCt(vg) + 1
If Fg = Left(sqr3(vg), 1) Then
For dirVg = 1 To 2
goodVg = True
If dirVg = 1 And Mid(sqr3(vg), 2, 1) = Dg Then
Eg = Mid(sqr3(vg), 3, 1)
ElseIf dirVg = 2 And Mid(sqr3(vg), 3, 1) = Dg Then
Eg = Mid(sqr3(vg), 2, 1)
Else
goodVg = False
End If
If goodVg Then
For E = 1 To numSqr4
If Left(sqr4(E), 1) = Eg And had4(E) = False Then
For dirE = 1 To 2
goodE = True
If dirE = 1 And Eh = Mid(sqr4(E), 4, 1) Then
Ef = Mid(sqr4(E), 2, 1)
Ee = Mid(sqr4(E), 3, 1)
ElseIf dirE = 2 And Eh = Mid(sqr4(E), 2, 1) Then
Ee = Mid(sqr4(E), 3, 1)
Ef = Mid(sqr4(E), 4, 1)
Else
goodE = False
End If ' new4 E
If goodE Then
' chw = TextWidth("W"): chh = TextHeight("W")
' CurrentX = 4 * chw: CurrentY = 13 * chh
' Print Ae; " "; Af
' CurrentX = 4 * chw: CurrentY = 15 * chh
' Print Aa; " "; Ab
' CurrentX = 1 * chw: CurrentY = 17 * chh
' Print Be; " "; Ba; " "; Ca; " "; Cb; " "; Db; " "; Df; " "; Ef; " "; Ee
' CurrentX = 1 * chw: CurrentY = 19 * chh
' Print Bh; " "; Bd; " "; Cd; " "; Cc; " "; Dc; " "; Dg; " "; Eg; " "; Eh
' CurrentX = 4 * chw: CurrentY = 21 * chh
' Print Fd; " "; Fc
' CurrentX = 4 * chw: CurrentY = 23 * chh
' Print Fh; " "; Fg
DoEvents
ctB = ctB + 1
tr1 = Ef & Df & Af
tr2 = Ef & Af & Df
tr3 = Ee & Ae & Be
tr4 = Ee & Be & Ae
If onList(tr1) Or onList(tr2) Then
If onList(tr3) Or onList(tr4) Then
Print #2, " "; Ae; Af
Print #2, " "; Aa; Ab
Print #2, Be; Ba; Ca; Cb; Db; Df; Ef; Ee
Print #2, Bh; Bd; Cd; Cc; Dc; Dg; Eg; Eh
Print #2, " "; Fd; Fc
Print #2, " "; Fh; Fg
Print #2, sqr4(A); " "; sqr4(B); " "; sqr4(C); " "; sqr4(D); " "; sqr4(E); " "; sqr4(F)
Print #2, sqr3(va); " "; sqr3(vertb); " "; sqr3(vc); " "; sqr3(vd); " "; sqr3(ve); " "; sqr3(vf); " "; sqr3(vg); " "; sqr3(vh)
For iCtr = 1 To numSqr3
thisCt = vCt(iCtr)
If tr1 = sqr3(iCtr) Or tr2 = sqr3(iCtr) Then thisCt = thisCt + 1
If tr3 = sqr3(iCtr) Or tr4 = sqr3(iCtr) Then thisCt = thisCt + 1
If thisCt > 0 Then
Print #2, sqr3(iCtr); thisCt; " ";
End If
Next
Print #2,: Print #2,
ctSol = ctSol + 1
End If ' tr1 or tr2
End If ' tr1 or tr2
End If ' goodE
Next dirE
End If ' Eg matches
Next E
End If ' goodVg
Next dirVg
End If ' Fg is first digit of vg
vCt(vg) = vCt(vg) - 1
Next vg
End If ' goodVh
Next dirVh
End If ' Fh is first digit of vh
vCt(vh) = vCt(vh) - 1
Next vh
End If ' goodF
Next dirF
had4(F) = False
End If ' Fc matches
Next F
End If ' good dirVc
Next dirVc
vCt(vc) = vCt(vc) - 1
Next vc
had4(D) = False
Next dirD
End If ' D begins with Db
Next D
End If ' good vertb
Next dirVb
vCt(vertb) = vCt(vertb) - 1
Next vertb
had4(C) = False
End If ' goodC
Next dirC
End If ' C fits Cd
End If 'had4(C) false
Next C
Next
End If ' sqr3(vd) begins with Bd
vCt(vd) = vCt(vd) - 1
Next vd
had4(B) = False
End If ' goodB
Next dirB
End If ' had4(B)=false
Next B
End If ' goodVa
Next dirVa
vCt(va) = vCt(va) - 1
Next va
Next dirA
had4(A) = False
Next A
Print "end"; ctB
Close 2
End Sub
Function onList(s)
For i = 1 To numSqr3
If s = sqr3(i) Then onList = True: Exit Function
Next
onList = False
End Function
I had to use variable vertb instead of vb, as Visual Basic kept insisting on capitalizing VB, even though it's not a reserved word in VB, only the abbreviation for the language.
The program found 63 solutions with just one repeated vertex square and 30 with no repeated vertex squares.
An example with no repeated vertex squares:
52
11
61 24 89 52
56 61 64 42
73
21
A=1521 B=6561 C=6241 D=8649 E=4225 F=3721
a=121 b=841 c=361 d=676 e=256 f=529 g=144 h=225
121 1 144 1 225 1 256 1 361 1 529 1 676 1 841 1
The last line has the vertex counts that enabled me to weed out duplicates beyond those allowed.
An example of one duplicated vertex square:
52
12
24 44 31 16
64 14 48 47
41
67
A=1225 B=4624 C=1444 D=3481 E=4761 F=1764
a=441 b=324 c=144 d=441 e=625 f=121 g=784 h=676
121 1 144 1 324 1 441 2 625 1 676 1 784 1
|
|
Posted by Charlie
on 2008-05-02 17:10:57 |




