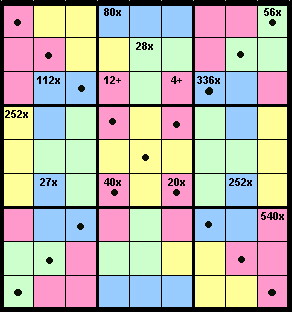
Place the numbers 1 to 9 once in each row, column,
long diagonal (marked with a heavy dot) and every 3x3 grid.
The '
cage' inclusions (individually coloured regions) indicate the sum or the product of the numbers in those cells.
Unlike Killer Sudoku, the same number may appear more than once in a cage. So, 36x in a cage which overlaps the 3x3 grids may contain two 6s and a 1.
 My inspiration for this puzzle came from a variety of puzzles posted by Pete and Will at http://sudexel.com/forum/index.php
My inspiration for this puzzle came from a variety of puzzles posted by Pete and Will at http://sudexel.com/forum/index.php
My thanks goes to brianjn for his hard work in producing the graphic.
(In reply to
re(2): Solution by Dej Mar)
I assume that outside the 9 x 9 array you had cells referencing the "annotated" cages.
In the first few formats that Josie sent to me the "tableau" was much more sophisticated. However, for the venture on which you embarked the 9 x 9 array could readily be transformed to an x-y grid of 9 x 18 with each 1 x 2 cell equating to a 1 x 1 in the 9 x 9 array. The top cell of one of those 1 x 2's per annotated cage would hold the formula for referenced cells to give the value suggested. Maybe an =IF() referral to an outside location to test the "true" value.
If Josie offers something akin to this again, and it's accepted, those thoughts might be a tool addition. I'm going to play with those thoughts.
|
|
Posted by brianjn
on 2008-05-30 01:17:09 |




