Please reflect upon "Gyro-Lattice 1 - Arrows" at puzzle 6061.

The rotations available are: - [V] vertical [red] - [H] horizontal [magenta] - [R] right-down diagonal [green] - [L] left-down diagonal [salmon] The assigned operations programmed for this are:

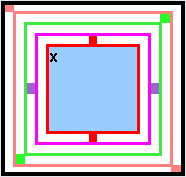
V ±: +/- 1    H ±: ×/÷ 2     R ±: x2/√    L ±: ceil/floor  

("+" represents the high value, ie, V+ = +1; V- = -1).

Using this syntax how can you arrive at each output from the given input value?
Use values like H+, V-, L+ to fill in my table.
Oh, for each assigned task each operation (with a corresponding "±" value) is required.

In the first row we get:

 100 Op1[√] 10  Op2[+1] 11  Op3[*2] 22 Op4[floor] 22
 100  R-    10   V+     11   H+     22  L-        22

There will be more than one route to a destination.

	In	Op1	Op2	Op3	Op4	Out		In	Op1	Op2	Op3	Op4	Out
	100	R-	V+	H+	L-	22		7					4
	100					19		7					3
	100					14		47					9.592..
	100					4999		47					15
	100					6		47					1152

Each section is headed by the input and output. Following each such header is a list of sets of operations, with the letters on one line and the + or - sign beneath each corresponding letter. Each entry in the list will serve to transform the numbers. I don't see what this has to do with the actual gyro lattice however.

 100           22 
vrlh
+-++
lrvh
--++
lrvh
+-++
rlvh
--++
rlvh
-+++
rvhl
-++-
rvhl
-+++
rvlh
-+-+
rvlh
-+++

 100           19 
vrhl
--+-
lrhv
--+-
lrhv
+-+-
rhlv
-+--
rhlv
-++-
rhvl
-+--
rhvl
-+-+
rlhv
--+-
rlhv
-++-

 100           14 
vhrl
-+--
vhrl
++--
hrlv
+-+-
hrvl
+--+
hvrl
+---
hvrl
++--

 100           4999 
lrhv
-+--
lrhv
++--
rhlv
+---
rhlv
+-+-
rhvl
+---
rhvl
+--+
rlhv
+---
rlhv
++--
rvhl
+---

 100           6 
vrhl
+--+
hrlv
----
hrvl
----
lrhv
---+
lrhv
+--+
rhlv
---+
rhlv
--++
rhvl
--+-
rhvl
--++
rlhv
---+
rlhv
-+-+
rvhl
-+-+

 7             4 
vhrl
-+-+
vhrl
++--
vhrl
++-+
vlhr
+-+-
vlhr
+++-
vrhl
--+-
vrlh
---+
vrlh
+--+
hlvr
---+
hrlv
+--+
hrvl
+-+-
hvlr
---+
hvrl
+--+
hvrl
++-+
lvhr
-++-
lvhr
+++-
rhlv
-+--
rhvl
-+--
rlvh
-+-+
rvhl
--++
rvlh
--++
vhlr
++--
vhlr
+++-

 7             3 
vhrl
-+--
hlrv
-+-+
hrlv
--++
hrlv
+-+-
hrvl
--++
hrvl
+--+
hvrl
-+-+
hvrl
+---
hvrl
++--
rhlv
--++
rhvl
--++
rlhv
--+-
rvhl
--+-

 47            9.592 (approx)
vlhr
--+-
vlhr
-++-
lvhr
--+-
lvhr
+-+-
vhlr
-+--
vhlr
-++-

 47            15 
rhlv
-+++
rhvl
-+++
rlhv
-+++
rvhl
-++-

 47            1152 
vlrh
+-+-
vlrh
+++-
vrhl
++--
vrhl
++-+
vrlh
++--
vrlh
+++-
lvrh
-++-
lvrh
+++-

DECLARE SUB permute (a$)
DEFDBL A-Z
DATA 100,22, 100,19, 100,14, 100,4999, 100, 6
DATA 7,4, 7,3, 47,9.592, 47,15, 47,1152
CLS
OPEN "glat3val.txt" FOR OUTPUT AS #2
DO
 READ nIn, nOut: PRINT nIn, nOut: PRINT #2, nIn, nOut
 a$ = "vhrl": h$ = a$
 DO
   FOR sg1 = 0 TO 1
    sg(1) = sg1

   FOR sg2 = 0 TO 1
    sg(2) = sg2

   FOR sg3 = 0 TO 1
    sg(3) = sg3

   FOR sg4 = 0 TO 1
    sg(4) = sg4

    v = nIn
    FOR i = 1 TO 4
      SELECT CASE MID$(a$, i, 1)
        CASE "v"
         IF sg(i) THEN v = v + 1:  ELSE v = v - 1
        CASE "h"
         IF sg(i) THEN v = v * 2:  ELSE v = v / 2
        CASE "r"
         IF sg(i) THEN v = v * v:  ELSE v = SQR(v)
        CASE "l"
         IF sg(i) THEN v = -INT(-v):  ELSE v = INT(v)
      END SELECT
    NEXT i
    IF v = nOut OR nOut <> INT(nOut) AND INT(1000 * v + .5) = INT(1000 * nOut + .5) THEN
     PRINT a$
     PRINT #2, a$
     FOR i = 1 TO 4
      IF sg(i) THEN PRINT "+"; :  ELSE PRINT "-";
      IF sg(i) THEN PRINT #2, "+"; :  ELSE PRINT #2, "-";
     NEXT
     PRINT
     PRINT #2,
    END IF

   NEXT sg4

   NEXT sg3

   NEXT sg2

   NEXT sg1
   permute a$
 LOOP UNTIL a$ = h$
 PRINT
 PRINT #2,
LOOP
CLOSE

END

SUB permute (a$)
DEFINT A-Z
 x$ = ""
 FOR i = LEN(a$) TO 1 STEP -1
  l$ = x$
  x$ = MID$(a$, i, 1)
  IF x$ < l$ THEN EXIT FOR
 NEXT

 IF i = 0 THEN
  FOR j = 1 TO LEN(a$) \ 2
   x$ = MID$(a$, j, 1)
   MID$(a$, j, 1) = MID$(a$, LEN(a$) - j + 1, 1)
   MID$(a$, LEN(a$) - j + 1, 1) = x$
  NEXT
 ELSE
  FOR j = LEN(a$) TO i + 1 STEP -1
   IF MID$(a$, j, 1) > x$ THEN EXIT FOR
  NEXT
  MID$(a$, i, 1) = MID$(a$, j, 1)
  MID$(a$, j, 1) = x$
  FOR j = 1 TO (LEN(a$) - i) \ 2
   x$ = MID$(a$, i + j, 1)
   MID$(a$, i + j, 1) = MID$(a$, LEN(a$) - j + 1, 1)
   MID$(a$, LEN(a$) - j + 1, 1) = x$
  NEXT
 END IF
END SUB

 

Posted by Charlie on 2008-06-23 02:25:44