This array, which I have begun to colour, is the top part of a "Four Colour Map" with rows extending beyond the borders given.

The boundaries displayed in Rows 1 to 4 are repeated down the map, ie, Row 5 has the same boundaries as Row 1, but may be coloured differently.


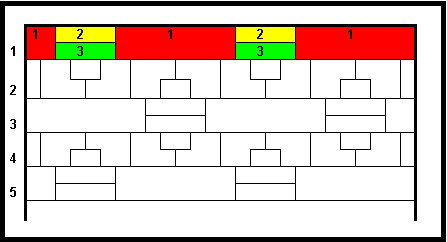
In colouring this map no two regions of the same colour may have part of a border in common and a row pattern is repeated across the row.

Tasks:
1. At which row could I soonest expect to see the exact colouring and layout pattern of Row 1?

2. Suggest a topologically simpler and what probably is a more aesthetic geometric layout for the vertices of my map?

The soonest possible to see the exact colouring and layout pattern of Row 1 is Row 5. The following is a pattern that achieves this:
Row 1: 11222211111111222211111111
       11333311111111333311111111
Row 2: 42211442224442211442224442
       42224442211442224442211442
Row 3: 11111111333311111111333311
       11111111222211111111222211
Row 4: 43334443311443334443311443
       43311443334443311443334443
Row 5: 11222211111111222211111111
       11333311111111333311111111

If Row 5 is required to be colored differently than Row 1, then the soonest that would be possible for a row to be able to have the coloring and layout pattern of Row 1 would be Row 9. Yet, perhaps the question was meant to be asking what is the maximum number of rows that can exist with no repeated coloring and layout pattern.  In this case, I have not yet discovered an answer. 

Edited on July 8, 2008, 11:28 pm

Posted by Dej Mar on 2008-07-08 19:28:08