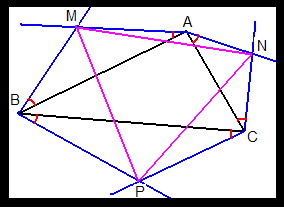
Let ABC be any triangle you draw.

From each vertex, draw two lines outside the triangle, each one at 30' (red arcs) with the sides that meet each other in the vertex.

These 6 lines cross, two by two, at 3 points, named M, N, and P.

Prove that, no matter what triangle ABC you draw initially, the triangle MNP is always equilateral.

Let the letters A, B, C, M, N, and P denote complex
numbers. The givens of the problem imply that

   N - A = Z_30*(C - A)

   M - B = Z_30*(A - B)

   P - C = Z_30*(B - C)

where Z_30 = 1/2 + i*sqrt(3)/6.

With a lot of tedious math it can be shown that

   M - P = Z_60*(N - P)

where Z_60 = 1/2 + i*sqrt(3)/2.
 
Therefore, MNP is an equilateral triangle.

Note: Multiplying a complex number by
   
      Z_30: rotates it by 30 degrees CCW and
            divides its argument by sqrt(3)

      Z_60: rotates it by 60 degrees CCW

Posted by Bractals on 2008-10-14 15:52:10