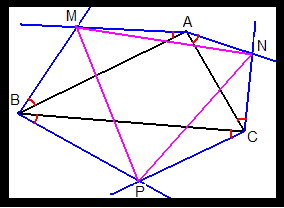
From each vertex, draw two lines outside the triangle, each one at 30' (red arcs) with the sides that meet each other in the vertex.
These 6 lines cross, two by two, at 3 points, named M, N, and P.
Prove that, no matter what triangle ABC you draw initially, the triangle MNP is always equilateral.